Solutions to Homework Tasks

Task 1 (2 points): First-order logic

Consider the signature Σ = (Int, +, *, 0, 1), where +, *: Int x Int -> Int are binary function symbols and 0, 1: Int are constant function symbols.

Give a Σ-formula F expressing that $x<y$ holds modulo the theory of Peano arithmetic (without using the symbol <!). That is, for every interpretation $\mathfrak{I}$ in which all symbols have the canonical meaning, $\mathfrak{I}\models F$ should hold if and only if the integer $\mathfrak{I}(x)$ is strictly less than $\mathfrak{I}(y)$.

Your formula should not have any free variables other than $x$ and $y$.

Solution

Intuitively, $x<y$ holds iff we can find a natural number $z>0$ such that $x+z==z$ is true.

If we assume, for the moment, that Σ would use the sort Nat of natural numbers instead of arbitrary integers, then we could use the formula

exists z: Nat :: !(z == 0) && x + z == y

However, we need to consider the sort Int of arbitrary integers. One approach is to use the above formula, with z no of sort Int, and then adding a constraint that z is a natural number.

For example, we can express this property using Lagrange's four-square theorem, which states that every natural number can be represented as the sum of four (necessarily non-negative) integer squares.

This yields the following formula

exists z:Int, a:Int, b:Int, c: Int, d: Int ::
    z == a*a + b*b + c*c + d*d &&
    !(z == 0) && x + z == y

Task 2 (5 points): Axiomatic Systems

In the lecture, we introduced axiomatic systems to specify only those Σ-structures that we are interested in. The goal of this task is to find suitable axiomatic systems for a few interesting classes of Σ-structures.

First, consider the signature Σ = (V, E), where V is some sort. Moreover, E: V x V is a binary relational symbol.

(a) Give an axiomatic system AX describing all undirected graphs without self-loops.

Solution

// the edge relation E is symmetric for undirected graphs
forall x: V, y: V :: E(x,y) ==> !(x == y)

// self-loops are not allowed
forall x: V, y: V :: E(x,y) ==> E(y,x)

(b) Give an axiomatic system AX describing all structures Σ = (V, E) in which E represents a total order of the elements of V.

Solution

// reflexivity
forall x:V :: E(x,x)

// antisymmetry
forall x:V, y:V :: E(x,y) && E(y,x) ==> x = y

// transitivity
forall x: V, y: V, z: V :: E(x,y) && E(y,z) ==> E(x,z)

// totality
forall x: V, y: V :: E(x,y) || E(y,x)

(c) Give an axiomatic system AX describing all structures with more than two elements, that is, those structures Σ = (V, E) such that |V| > 2.

Solution

exists x: V, y: V, z: V :: !(x == y) && !(x == z) && !(y == z)

Now, consider the signature Σ = (Array, Int, get, put), where Array and Int are sorts. Moreover, get: Array x Int -> Int and put: Array x Int x Int -> Array are function symbols.

(d) Give an axiomatic system AX describing (unbounded) arrays (elements of sort Array) of integers (elements of sort Int) using the above signature. Here, get(A, i) represents the i-th value of array A and put(A, i, v) represents the array which is the same as array A but with the i-th value set to v. Your axiomatic system should ensure that two arrays are considered equal if they contain the same elements.

Hint: Read the task carefully.

Solution

We first add an axiom that we retrieve the same values that we have previous put into an array:

forall A:Array :: 
    forall i:Int, v::Int ::
        get(put(A,i,v), i) == v

When retrieving a value, the outermost put function may also consider a different index. To ignore such a case, we can axiomatize that putting in values is commutative as long as we use different array indices:

forall A:Array :: 
    forall i:Int, v:Int, j:Int, w:Int ::
        i != j ==> put(put(A,i,v),j, w) == put(put(A,j,w),i,v)

Alternatively, we could explicitly ignore different indices for the get function:

forall A:Array :: 
    forall i:Int, v:Int, j:Int ::
        i != j ==> get(put(A,i,v),j) == get(A,j)

The last part requires careful reading of the task: "your axiomatic system should ensure that two arrays are considered equal if they contain the same elements".

The description only requires that two arrays have the same set of elements; the indices and cardinalities do not matter. A corresponding axiom would be

forall A:Array, B:Array ::
    (forall i:Int :: exists j:Int :: get(A,i) == get(B,j))
        ==> A == B

This axiom states what the task requires. However, we may actually want to also take the order and cardinalities into account when axiomatizing an actual array. We can use the following axiom for that:

forall A:Array, B:Array ::
    (forall i:Int :: get(A,i) == get(B,i))
        ==> A == B

Task 3 (3 points): Using an SMT solver

A large Danish company currently produces three kinds of products, let's call them product A, B, and C. The company wishes to reduce overhead by producing only two kinds of products in the future.

Your task is to use Z3 to evaluate whether this is possible given the companies production constraints listed below.

• The company needs to produce at least 100 products (of any kind) within 3 hours.
• The company needs to produce at least 5 products of kind A or kind B.
• The company needs to produce at least 10 products of kind C.
• To produce a product of kind A, B, and C, the company needs 1, 2, and 5 minutes, respectively.
• To produce a product of kind A, B, and C, the company needs to invest 3000, 2000, and 1000 DKK, respectively.
• The company wants to invest at most 300000 DKK.

Submit your encoding of the above problem in Z3 (using SMTLIB or one of the APIs, e.g. pySMT); briefly explain your constraints using inline comments.

Solution

; number of products of kind A, B, and C, respectively
(declare-const A Int)
(declare-const B Int)
(declare-const C Int)

; produce at least 100 products (of any kind) 
; within 3 hours (we ignore everything after that)
(assert (>= (+ A B C) 100 ))

; To produce a product of kind A, B, and C, the company needs 1, 2, and 5 minutes
; we cut off production after 180 minutes (3h)
(assert (>= 180 (+ (* A 1) (* B 2) (* C 5))))

; The company needs to produce at least 5 products of kind A or kind B.
(assert (or (<= 5 A) (<= 5 B)))
; ambiguity: could also be understood as (assert (<= 5 (+ A B)))

; The company needs to produce at least 10 products of kind C.
(assert (<= 10 C))

; To produce a product of kind A, B, and C, 
; the company needs to invest 3000, 2000, and 1000 DKK
; The company wants to invest at most 300000 DKK.
(assert (>= 300000 (+ (* A 3000) (* B 2000) (* C 1000))))

; a model now gives as the production numbers for each kind
; to check whether the company can omit a product, we can
; additionally assert that 0 products of one kind are produced
; and see if the formula remains satisfiable.

(push)
(echo "Can we drop producing A? (unsat means no)")
(assert (= A 0))
(check-sat)
(pop)

(push)
(echo "Can we drop producing B? (unsat means no)")
(assert (= B 0))
(check-sat)
(pop)

(push)
(echo "Can we drop producing B? (unsat means no)")
(assert (= C 0))
(check-sat)
(pop)

Task 4 (20 points): Akari

For this task, we consider a puzzle game with simple rules and challenging solutions called "Akari" or "Light Up". The rules are as follows:

• The game is played on a rectangular grid of walls (black tiles) and empty (white) tiles.
• Initially the whole grid is dark.
• The goal is to place lightbulbs on some of the empty tiles until all non-wall tiles are lit.
• Every lightbulb shines light in the 4 cardinal directions (up, down, left, right) until the light is stopped by a wall.
• Two lightbulbs are not allowed to shine light on each other.
• Some wall tiles may have a number (typically between 0 and 4) assigned to it, which indicates how many lightbulbs must be placed in the adjacent empty tiles.

If you want to get a feeling for the game, you can also play it online. Furthermore, here is a collection of example puzzles, together with solutions for the first few puzzles:

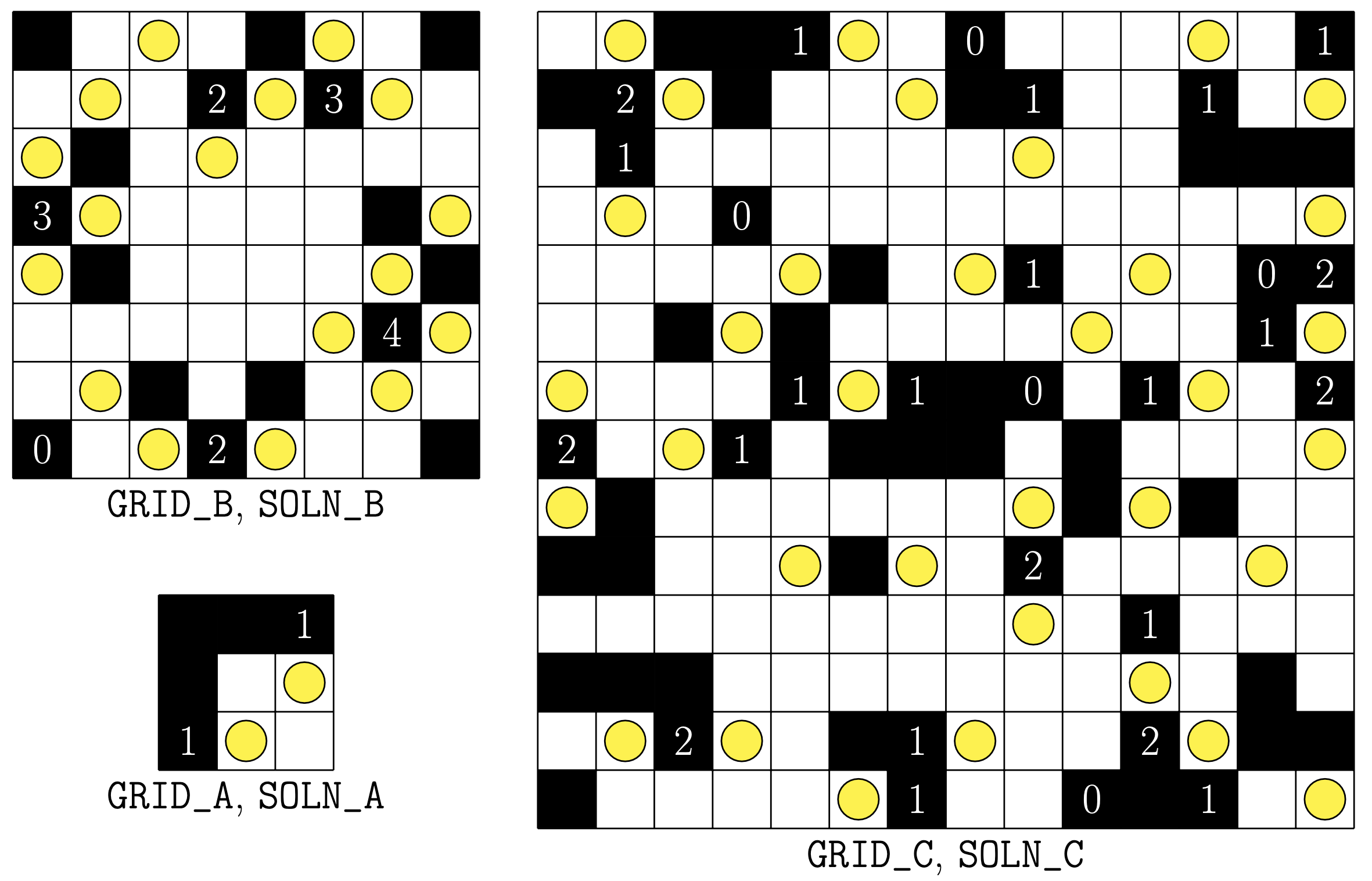
Your task is to implement a program that utilizes Z3 to solve arbitrary Akari puzzles, such as the ones illustrated above.

The above examples each have a unique solution but, in general, your implementation should find some solution. If there is no solution, it should report that as well.

Make sure that your code is well-documented. In particular, explain what each constraint that you give to the SMT solver means.

You can choose any language that you want to use. We provide you with two code skeletons, one using the python Z3 bindings and one using the rust Z3 bindings, respectively. Both code skeletons contain:

• An explanation of how puzzles are represented.
• An explanation of how solutions are represented.
• The function validate_solution which takes a puzzle and a solution and checks whether the solution is correct. You can use this function, together with the seven puzzles from above, which are also provided in the file, to test your implementation.
• An unimplemented function solve that you should implement.

Files:

Skeletons for Akari

Solution with comments